Principe de la réflectométrie

Reflectometry principle

Le principe de base de la réflectométrie est de supposer qu'il existe une position dans le plasma où la fréquence plasma devient plus grande que la fréquence de l'onde. L'onde ne pouvant plus se propager se refléchit au point où (coupure). Il est possible connaissant le temps de vol ou la phase pour une fréquence donnée équivalente à une densité de calculer la position de la coupure rc(w) dans le plasma. En conséquence de quoi il est possible de reconstruire le profil de densité du plasma en changeant la fréquence du réflectomètre. L'avantage de cette méthode est qu'elle ne perturbe pas le plasma.
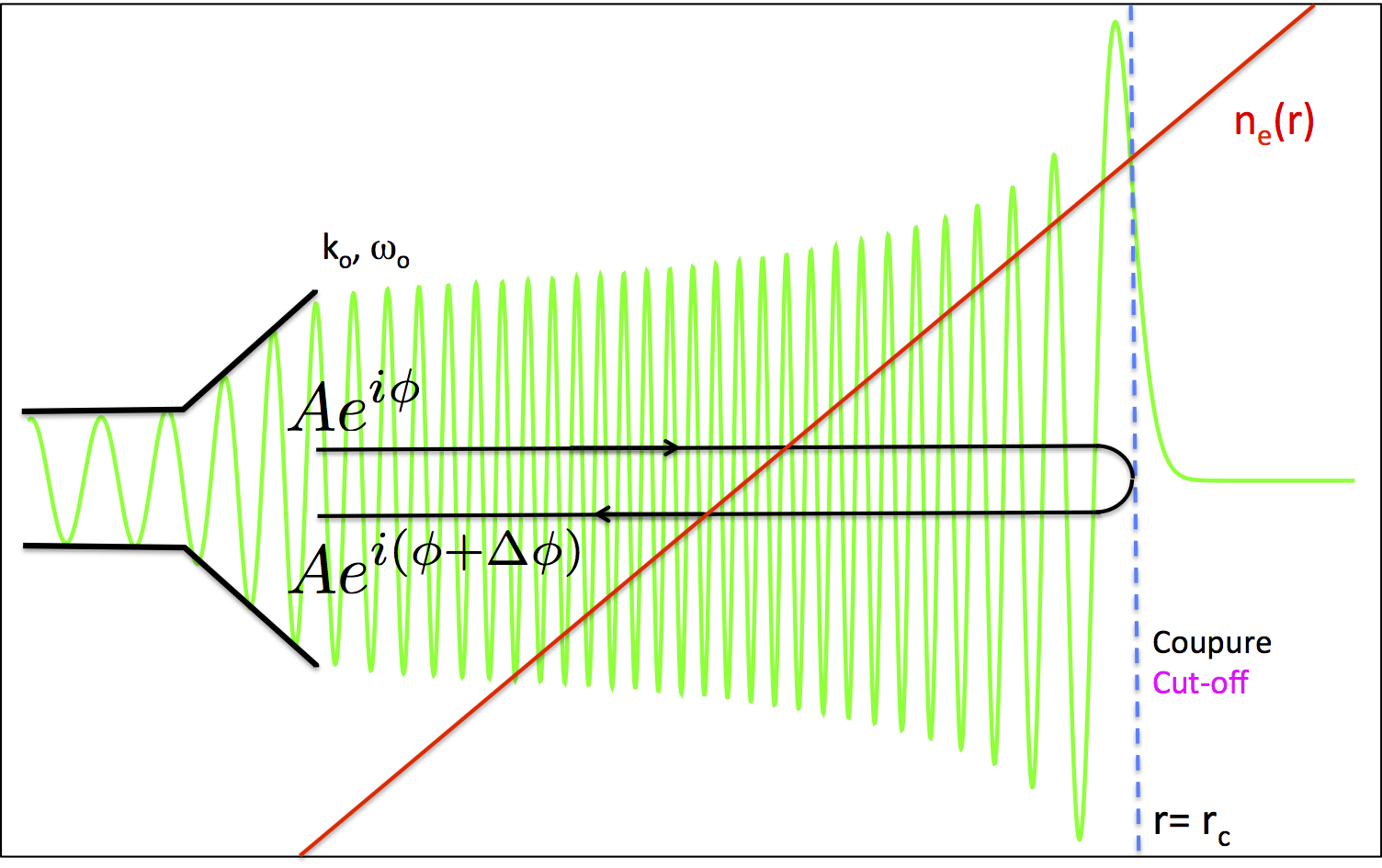
O-mode Reflectometry basic principle assumes that a cut-off layer exists at a given position where the plasma frequency becomes greater than the probing frequency. Above this position where that defiens also the cut-off layer. Knowing the time of flight or the phase varition for a given frequency it becomes possible to determine the cut-off position rc(w) in the probed plasma. Thus the density profile can be rebuilt by changing the probing frequency. This diagnostic is non-perturbative. Text and movies from S. Heuraux.

Figure1: Schéma de principe d'un réflectomètre "classique" pour une fréquence donnée wo,l'onde de sondage est en vert, le profil de densité est en rouge.
Figure 1: Scheme of the fix frequency reflectometry principle, the probing electric field in green and the density profile in red

Il est possible sous certaines conditions de caractériser les fluctuations de densité du plasma qui sont la cause de phénomènes de transport d'énergie dit anormaux (L'énergie fuit plus vite que les modèles de transport ne le prévoit d'où le qualificatif "anormal"). La réflectométrie devient alors un moyen de diagnostiquer les fluctuations de densité. C'est un sujet de recherche développé à l'IJL dans l'équipe plasmas chauds.
Under restricitions, the density fluctuations can be characterized, which are linked to the anomalous transport of the energy (the energy flows outside faster than neoclassical models predict. The reflectometry was proposed to diagnose the turbulence. That is one part of the diangostic Physics done at IJL in the hot plasmas team.

Pour illustrer nos propos, différentes animations seront présentés en plasma inhomogène
To illustrate our purposes movies showing different cases in inhomgeneous plasmas can be visualized.

(inhomogéne <=> milieu dont les caractéristiques dépendent de la position).
Inhomogeneous means medium with varying properties as a function of the position.

Réflectomètre "classique"

"Standard" Reflectometry

Cet appareil de mesure est basé sur une évaluation de phase. Pour ce faire, il est donc nécessaire que l'onde remplisse tout l'espace de l'émétteur recepteur à la couche de coupure (voir figure du paragraphe d'introduction). La variation de phase détectée est donnée par :
This instrument is based on a phase measurement. To do it, the wave has to fulfil all the space between the emitter and the receiver, and the cut-off layer (have look at Fig 1 in the introduction). The measured phase is described analytically by:

où x c est la position de coupure dans le plasma pour la fréquence n, et k le veccteur d'onde (renvoi vers la relation de dispersion). Une inversion d'Abel est donc nécessaire pour reconstruire le profil de densité et les positions des différentes coupures sont données par
where xc is the cut-off position in the plasma corresponding to the frequency n, and k the wavenumber (cf the dispersion relation). To rebuild the density profile an Abel's inversion is necessary where the cut-off positions are given by:

où f représente la variable d'integration équivalente à la fréquence et la dérivée partielle de la variation de phase par rapport à f.
where f is a variable for the integration and can be seen as the frequency, and the frequency partial derivative of the phase variation versus f.

Le problème de cette méthode est que l'on est suppose que le plasma conserve son profil durant le temps de la mesure. Bien entendu, cela suppose aussi que la variation de phase mesurée n'est pas perturbée par un autre phénomène physique. Un moyen de réduire le temps d'interaction de l'onde avec le plasma pour effectuer la mesure est d'envoyer un pulse EM dans le plasma et de mesurer son temps de vol de l'émetteur au recepteur. C'est cette technique qui a été utilisée pour mesurer la densité de l'ionosphère.
To use this technique, the density profile is assumed frozen over the probing time. Of course it is also assumed that nothing perturbs the phase variation measured. Another wave to probe on shirt time is to launch an electromagnetic pulse and to measure its time of flight between the emitter and the receiver. This was a way to probe the ionosphere and to rebuild its density profile.

Réflectométrie de pulse

Pulse Reflectometry

Mesurer le temps de vol n'est pas une technique facile quand on cherche à reconstruire des profils de densité élevée c'est-à-dire de l'ordre de 10 20 pm -3 au centre. La gamme de fréquence correspondante se situe vers 20-100 GHz. Dans cette bande de fréquence, on sait seulement détecter le retour du pulse. Il est donc nécessaire d'effectuer des simulations de propagation de pulse pour comprendre les érreurs qui peuvent apparaître durant les mesures. Un peu de théorie, le temps de vol t du pulse dans le plasma est donné par l'intégrale de dx/v g (x) (temps nécessaire pour parcourir la distance dx à la vitesse v g(x) (renvoi vers vitesse de groupe) ). Ce calcul intégrale est obligatoire car la vitesse de groupe vg n'est pas une constante le long du trajet suivi par le pulse et donne l'expression suivante pour le temps de vol :
Using the time of flight measurement to rebuild the denity profile at high density (10^20 m-3) is not an easy task due to the fact that the needed frequency bandwidth is over 20-100 GHz range for O-mode and twice for X-mode. At these frequencies the hardware permits to detect a threshold associated to the backward pulse and not the shape of it. To understand the dispersion of the measurements "full-wave" simulations are required to evaluate the meaning of the errror barrs. A bit of theory to know what is the group velocity and its use to determine the time fo flight. The time of flight corresponds to the time range needed to cross the plasma from the edge to the cut-off layer and to reach again the plasma edge. The analytical definition is given by the integral of 1/vg(r) along the path of the pulse into the plasma. As the group velocity is a function of the position an evaluation of the integral is required and writes as:

.

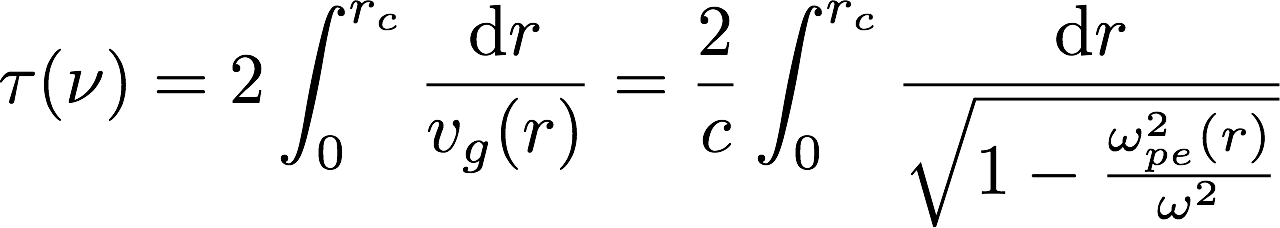Il est possible de relier le temps de vol à la phase en remarquant que si l'on dérive l'expression integrale de la phase par rapport à w on re trouve l'expression intégrale du temps de vol d'où la relation:
The time of flight is linked to the phase variations through its frequency derivative, so the expression of the time of flight is written as: :

En effecutant le changment de variable w = 2f et la substitution de la dérivée partielle de la phase par le temps de vol dans l'expression de l'inversion d'Abel, on obtient l'expression de l'inversion d'Abel en reflectométrie de pulse qui devient :
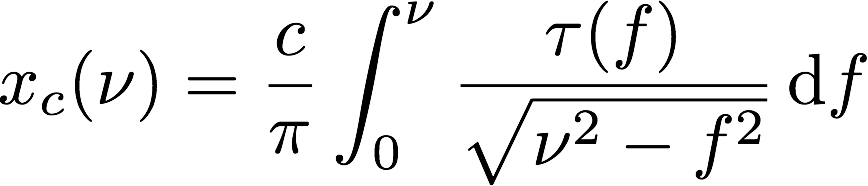Changing the variable w=2f and substituting the partial derivative of phase variations by the time of flight in the Abel's inversion, the cut-off position is thus determined using :

.

Pour mieux appréhender ces différentes notions des animations sont proposées ainsi qu'un schéma de principe.
To have a better feeling on these different notions movies can be animated and had a look at Fig.2

 

 

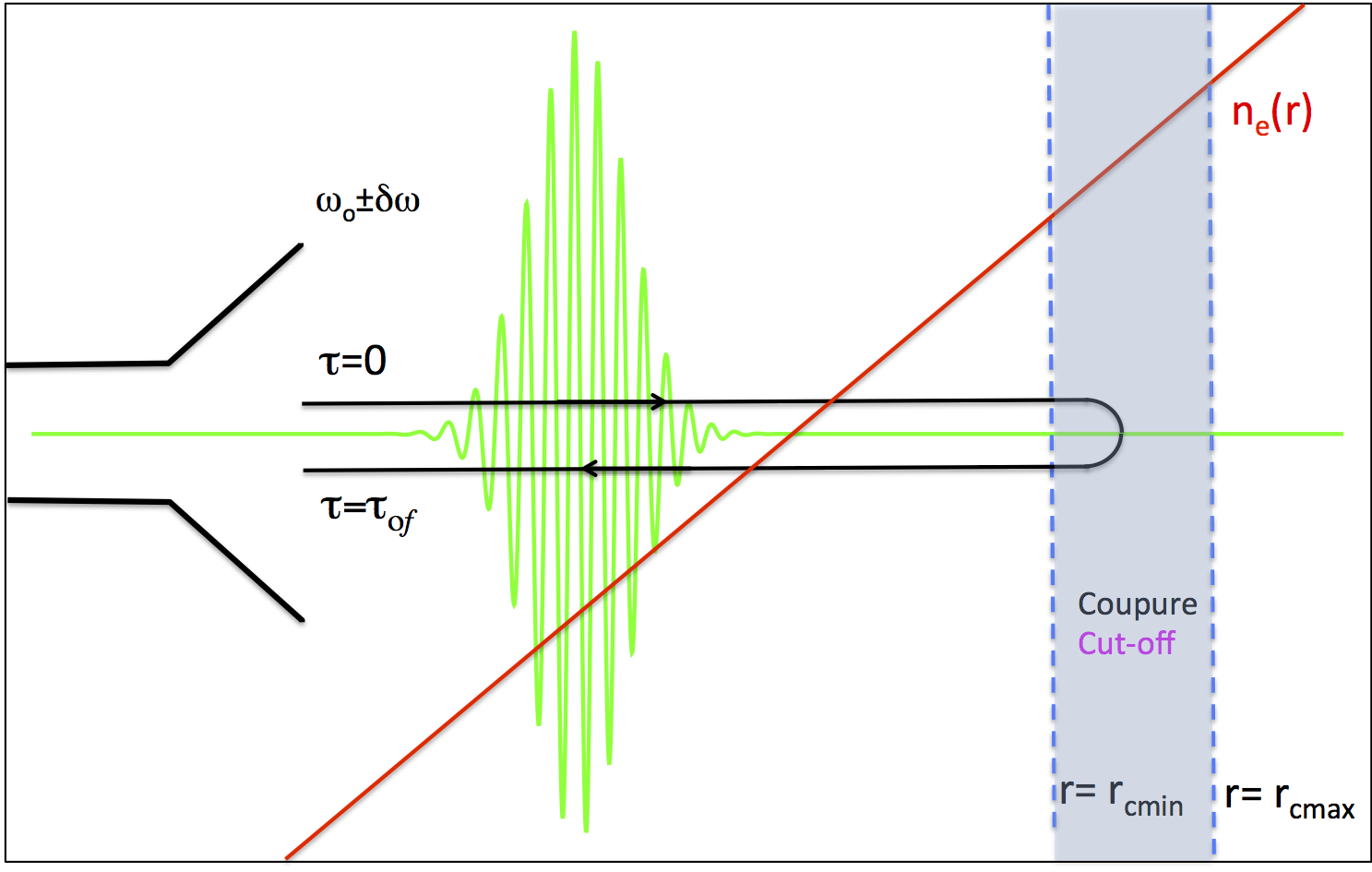
Figue 2: Schéma de principe de la réflectométrie de pulse où est grisée la zone dans laquelle le pulse se réfléchit en bleu sont représentées les coupures correspondant aux valeurs extermes de la fréquence contenues dans le spectre en fréquence du pulse.
Figure 2: Scheme of the Pulse reflectometry principle where the grey area indicates the region over which the pulse is reflected. The dashed blue lines represent the border of the reflection zone associated to the frequency bandwidth of the frequency spectrum of the probing pulse.

La première animation concerne la propagation d'un pulse gaussien de largeur modéré (une dizaine de longueur d'onde).
The first movie shows the time evolution (propagation) of a Gaussian pulse of 10 vacuum wavelengths width.

Au début le pulse est dans le vide, puis il rentre dans le plasma où sa longueur d'onde croit jusqu'à atteindre le point de réflexion. Il est possible de constater que les longueurs d'onde les plus grandes se réfléchissent d'abord et qu'une fois que le pulse retourne dans le vide sa largeur s'est accrue. Cet élargissement est lié à la dispersion . (renvoi vers effets de la dispersion). La dispersion ne peut exister que si le pulse est composé de plusieurs longueurs d'onde ( spectre ) (renvoi vers différents types de fluctuations) ce qui est le cas d'un pulse gaussien et si la vitesse de propagation dépend de la longueur d'onde (les hautes fréquences se propagent plus vite dans un plasma isotrope que les basses fréquences). Pour illustrer ce propos, la deuxième animation montre un pulse court (largeur plus petite que la longueur d'onde de la porteuse) qui est construit à partir d'un grand nombre de longueur d'onde ( spectre large (renvoi vers différents types de fluctuations) .
At the beginning the pulse propgates in vacuum without dispersion, when it enters in a plasma the wavelength increases until the cut-off layer is reached. A careful look permits to observe that the longest wavelengths are reflected first, and the when the pulse goes back in vacuum its width is greater. This widening corresponds to the dispersion effects, and that only possible if the pulse is built from a continuous set of different frequencies, which corresponds to the frequency spectrum. Thas is the case of Gaussian pulse. However this needs also that each frequency has its own group velocity, which is the case in plasmas. For example, the O-mode properties are that the higher frequency moves faster than the lower one if the considered frequencies are above the local plasma frequency. To illustrate the dispersion effects a short (width smaller than the vacuum wevelength) pulse with a wide frequency spectrum is launched. The last case correponds to the so-called ultra-short pulse.

 

On constate que le pulse pénètre plus loin dans le plasma et s'étale beaucoup plus que le cas précédent. D'ailleurs la longueur d'onde la plus grande est en opposition de phase par rapport au pulse incident. Cette constatation a été expliquée par T.H. Stix à l'aide de Eq(86) p 379 dans la 2ème édition du livre "waves in plasmas" éd AIP 1992. Ce dernier exemple correspond à un autre de type reflectomètre (pulse ultra-court).
In addition the shortest pulse goes deeper in the plasma and is spreaded faster than the previous case. One can see also that the phase of the reflected wave is opposite the incident one, this was explained by H. Stix (see Eq.(86) p379 2nd edition of the book entitled "Waves in plasmas" AIP 1992).

Autres types de reflectomètres

Other kinds of reflectometers

Les autres types de réflectomètres sont décrits dans l'article de C Laviron et al . Commençons par celui qui se rapproche le plus de la réflectométrie "classique" est le réflectomètre à balayage continu en fréquence avec une détection hétérodyne dont l'exemplaire le plus performant se trouve sur Le tokamak Tore Supra (renvoi à l'adresse de TS). Vient ensuite le reflectomètre à modulation d'amplitude où l'onde de sondage de fréquence variable est émise avec une puissance modulée à une fréquence fixe qui permet d'améliorer la dédection de la phase et la modulation de fréquence a le même role. Le reflectomètre à modulation de fréquence à amplitude constante permet lui aussi d'améliorer dans certains cas la détection de la phase. Le reflectomèrte à différence de fréquence constante explore simultanément deux couches de coupures distantes de 3-5 mm ce qui en théorie permet de supprimer les effets de turbulence sur le signal. Les différents réflectomètres déjà présentés suppose que le plasma évolue lentement (quasi-stationnaire sur des temps de l'ordre de 1-10 ms). Les méthodes s'affranchissent de cette contrainte mais elle réclament de faire des moyennes pour reconstruire des profils.
The other kinds of reflectometersare described in the Laviron's paper. The first one corresponds to an extension of the "standard" reflectometer where the frequency is swept linearly and heterodyne detection is used. The most efficient one is developed on Tore Supra tokamak at Cadarache. Another one, less used now, is based on amplitude modulation at fix frequency of changeable frequency of the carrier. The advantage of such method is to provide a better evaluation of the phase variations, this is also the case for the frequency modulation. So, the last purpose indicates that a frequency modulation reflectometer exists at constant launching power. However it becomes very complicated to work with ultra-fast frequency hopping system. After comes the correlation reflectometer, which works simultanously with two probing frequencies. Here two kinds exist one works at fix frequency difference and both are swept in frequencies, and the second one works with a fix frequency and the second probing wave is swept in frequency. New devolpments in theory and hardware permit to access to turbulence properties. But all the interpretation model assumes that the plasma is stationary over the probing time that is to say 1-10 ms. To overcome this assumption it is possible to use averging to rebuild the wanted profile.

la réflectométrie standard requière des conditions pour lesquelles le champ électrique de l'onde incidente et réfléchie se superposent ce qui conduit comme on le voit à la mise en place d'un système d'onde stationnaire. Pour cela il faut que la durée d'émission ?t de l'onde sonde soit plus grande que 4xc/c pour un profil de densité linéaire. Il est à noter que la structure du champ total est solution d'une équation d'Helmholtz qui s'écrit:
The standard reflectometry called FMCW requires conditions for which the incident and reflected are superimposed, which drives as one can see an oscillation. For that it is needed that the emission time ?t is greater than 4xc/c for a linear density profile. Notice that the total electric field is a solution of a Helmholtz equation, written as following:

.

La méthode compression radar consiste à envoyer d'une bande de fréquence sur un temps bref avec l'avantage d'avoir une puissance de sortie pour chaque fréquence quasi-constant. La reflectométrie de pulse ultra-court suit une voie similaire qui est l'envoi en même temps une large bande de fréquence mais avec une distribution de puissance sur les différentes fréquences qui dépend la forme du pulse de sondage se qui pose des problèmes de détection. Ces deux dernières techniques sont en cours d'étude.
The pulse compression method uses a frequency bandwidth on a short time confering the advantage to work at constant amplitude for each frequency. The same way is used for the ultra-short pulse reflectometry but here the frequency spectrum depends on the pulse shape that introduces problems for the detection and measurements. Slow progresses are done on these kinds of reflectometers. The ultra-fast sweep frequency becomes the best system and would be the only one if the phase synchronization is maintained from sweep to sweep is obtained the possibilities will become enormous, correlation reflectometry tools can be directly applied on these data as the other tools developed for the different kinds of reflectometers.

Ref: C Laviron, A.J.H. Donné,M.E. Manso and J. Sanchez " Reflectometry techniques for density profile measurements on fusion plasmas" Plasma Phys Cont Fusion, 38 (1996) 905.

Modélisations de l'utilisation de reflectomètres
Modeling of the use of the different reflectometers.

différents types de fluctuations de densité
different kinds of density fluctuations

conditions de détection
conditions for the detection

modèle avec des fluctuations de faible amplitude (approximation de Born)
Modeling with low level of the turbulence (under Born approximation)

modèle avec des fluctuations de grande amplitude.
Modeling with high level of the turbulence

Quelques applications :
Some applications:



retour-back